1. 多项式回归
将黑盒中的系统假设为多项式函数。

设系统的输入为 x,输出为 y,用多项式 f(x)≡a0+a1x+a2x2+⋯+an−1xn−1 去拟合。
得矩阵方程:Ax=b,其中 A 为 Vandermonde 矩阵,b 为输出向量。
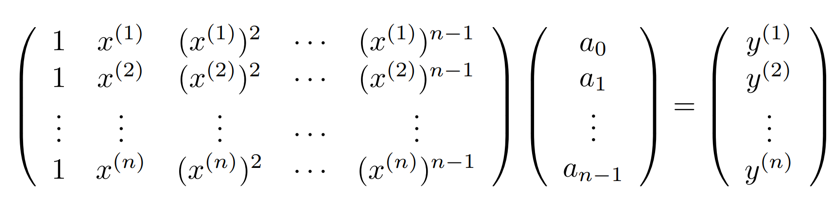
2. 最小二乘法
对于多于 n 个数据点的情况,使用最小二乘法,
min∥Ax−b∥22
对 x 求梯度,转化为求解 ATAx=ATb. 其中称 ATA 为Gram 矩阵。
3. Tikhonov 正则化
对于 Ax=b 的情况,使用 Tikhonov 正则化方法来求解:
min∥Ax−b∥22+λ∥x∥22
其中 λ 为正则化参数(惩罚因子),满足 0<λ<<1,使得结果不会产生过拟合。
求梯度后得到 (ATA+λI)x=ATb,解之即可。
[!TIP]
- Guassian: minx∥Ax−b∥22+α∥x∥22.
- Lasso: minx∥Ax−b∥22+β∥x∥1.
- Elastic net: minx∥Ax−b∥22+α∥x∥22+β∥x∥1.
4. Cholesky 分解
对于
 令
令
E=(1/c11−c111v0TI(n−1)×(n−1))
则
ECET=(100TC11)
如此操作多次,可得 C=LLT 中的 L=∏i=1nEi−1
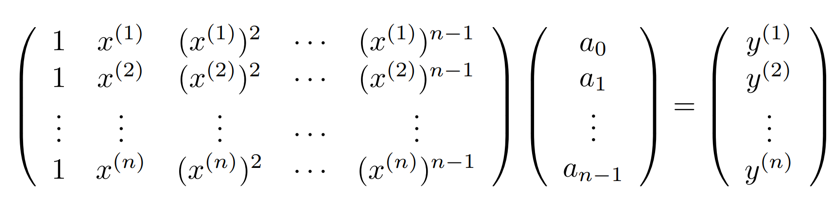
令