概率复习

1. 概率复习

1.1 样本空间

一个随机试验的所有可能结果的集合。

1.2 事件

样本空间的子集。

1.3 概率

概率是一个将事件集合映射到 $[0,1]$ 的函数。

$$P:2^\Omega \to [0,1]$$

满足Kolmogorov 公理：

1. 非负性：$P(A) \ge 0$
2. 规范性：$P(\Omega) = 1$
3. 可列可加性：$A_i \cap A_j = \emptyset \Rightarrow P(\bigcup A_i) = \sum P(A_i)$

1.4 随机变量

A random variable is a function that maps from the sample space to a measurable space.

1.5 条件独立

给定两个随机变量 $X$ 和 $Y$，若对于给定随机变量 $Z$，有

$$P(X,Y|Z) = P(X|Z)P(Y|Z)$$

则称 $X$ 和 $Y$ 条件独立，记作 $X \perp\!\!\!\perp Y | Z$。

2. Bayes 理论

• 似然 $L(H|E)$ : $L(H|E) = P(E|H)$

2.1 Bayesian Networks

关注于：

• ==后验概率==：$Pr[Q|E_1=e_1, \cdots, E_k=e_k]$
• ==最大似然解释==：$\text{argmax}_q$ $Pr[Q=q|E_1=e_1, \cdots, E_k=e_k]$

先计算边缘概率，再使用 Bayes 法则

Bayes 网络定义：

1. 一个有向无环图（DAG）$G=(V=\{X_1,\cdots,X_n\},E)$
2. 一个条件概率分布 $P(X_i|Pa(X_i))$

一个 Bayes 网络代表一个联合分布的因子分解：

$$p(X_1,\cdots,X_n)=\prod^{n}_{i=1} p(X_i|Pa(X_i))$$

每个节点的条件概率分布是局部的，只依赖于该节点的父节点。

2.2 Bayes 网络举例

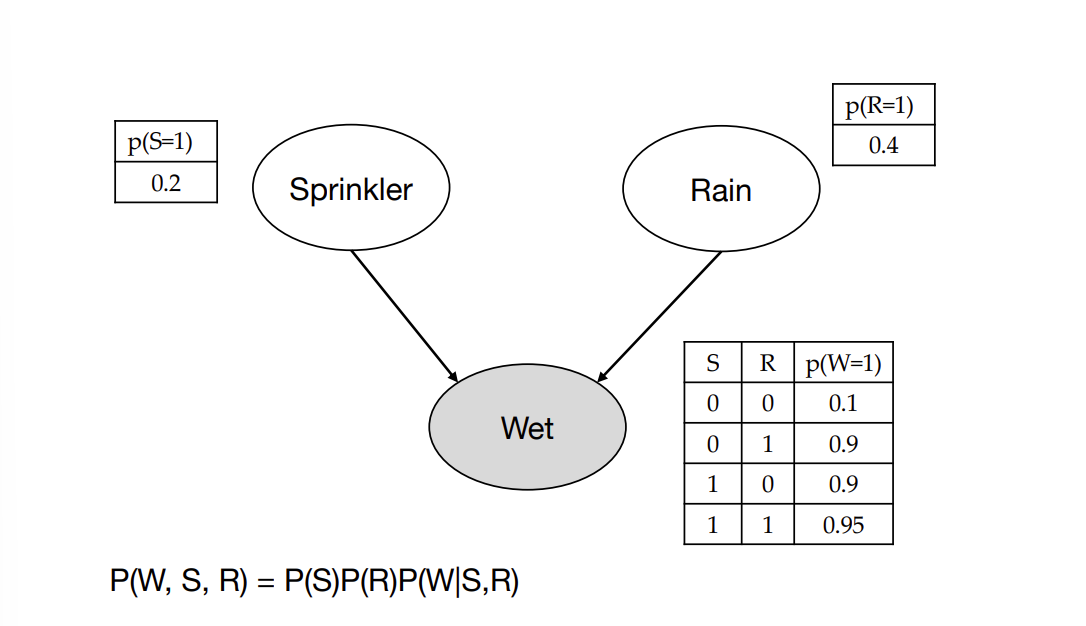父节点写后面，子节点写前面，最终结果乘起来。