跳到主要内容

矩阵的范数

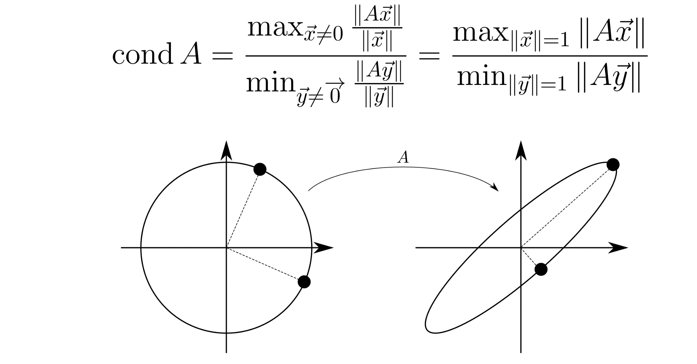
1. 范数​

考虑函数 ∥⋅∥:Rn→[0,∞)\Vert \cdot \Vert : \mathbb{R}^n\to \left[0,\infty\right) 满足：

  • ∥x⃗∥=0  ⟺  x⃗=0⃗\Vert \vec x\Vert=0 \iff \vec x = \vec 0
  • cx⃗=∣c∣∥x⃗∥∀c∈R,x⃗∈Rnc\vec{x} =|c|\parallel \vec{x}\parallel \quad \forall c\in R,\vec{x}\in \mathbb{R} ^n
  • ∥x⃗+y⃗∥≤∥x⃗∥+∥y⃗∥∀x⃗,y⃗∈Rn\Vert\vec{x}+\vec{y}\parallel \le \parallel \vec{x}\parallel +\parallel \vec{y}\parallel \quad \forall \vec{x},\vec{y}\in \mathbb{R} ^n 则称其为范数。

[!Tip] p-范数 ∥x⃗∥p=(∑k=1n∣xk∣p)1p\Vert\vec x\Vert_p = (\sum_{k=1}^n \lvert x_k\rvert^p)^{\frac{1}{p}}

2. 矩阵的范数​

定义矩阵的范数为 ∥An×n∥n≡max⁡x⃗∈Rn∥Ax⃗∥∥x⃗∥\Vert A_{n\times n} \Vert_{n}\equiv \max_{\vec x \in \mathbb{R}^n } \frac{\Vert A\vec x\Vert}{\Vert\vec x\Vert} 对于 n=1n=1，∥A∥1=max⁡j∑i∣aij∣\Vert A\Vert_1 = \max_j\sum_i\lvert a_{ij}\rvert 对于 n=2n=2，∥A∥2=max⁡{λ:AATx⃗=λx⃗}\Vert A\Vert_2 = \max\{\lambda:AA^T\vec x = \lambda \vec x\} 对于 n=∞n=\infty，∥A∥∞=max⁡i∑j∣aij∣\Vert A\Vert_\infty = \max_i\sum_j \lvert a_{ij}\rvert

450

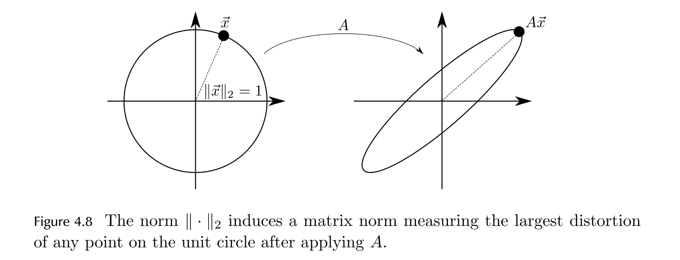
3. 误差估计​

(A+εδA)x⃗(ε)=b⃗+εδb⃗(A+\varepsilon \delta A)\vec{x}(\varepsilon) = \vec b + \varepsilon \delta \vec b

3.1 矩阵条件数​

condA=∥A∥∥A−1∥≡κ\text{cond} A = \Vert A\Vert\Vert A^{-1}\Vert \equiv \kappa

若 AA 不可逆，认为其条件数为无穷大。

condA=∥A∥∥A−1∥≥∥A∥∥A−1x⃗∥∥x⃗∥\mathrm{cond} A=\parallel A\parallel \left\| A^{-1} \right\| \ge \frac{\parallel A\parallel \left\| A^{-1}\vec{x} \right\|}{\parallel \vec{x}\parallel}

3.2 Relative change​

D≡∥δb⃗∥∥b⃗∥+∥δA∥∥A∥D\equiv \frac{\parallel \delta \vec{b}\parallel}{\parallel \vec{b}\parallel}+\frac{\parallel \delta A\parallel}{\parallel A\parallel}

进而，

∥x⃗(ε)−x⃗(0)∥∥x⃗(0)∥≤ε⋅D⋅κ+O(ε2)\frac{\parallel \vec{x}(\varepsilon )-\vec{x}(0)\parallel}{\parallel \vec{x}(0)\parallel}\le \varepsilon \cdot D\cdot \kappa +O\left( \varepsilon ^2 \right)

450