1. 求根问题
对于 f:R→R,找到 x∗ 使得 f(x∗)=0
x∗ 也可能是多变量
解法:
使用二分法:
- 对于连续函数 f(x),找到 l,r∈R 使得 f(l)f(r)<0
- 计算 c=2l+r, 若 f(c)=0, 结束
- 若 f(c)f(l)<0,采用 c 作为新的 r;否则,采用 c 作为新的 l
- 当 ∣r−l∣<ε 后,c 可以视为 x∗
2. 求不动点问题
不动点问题 f(x)=x 可以视为 f(x)−x=0 的求根问题。
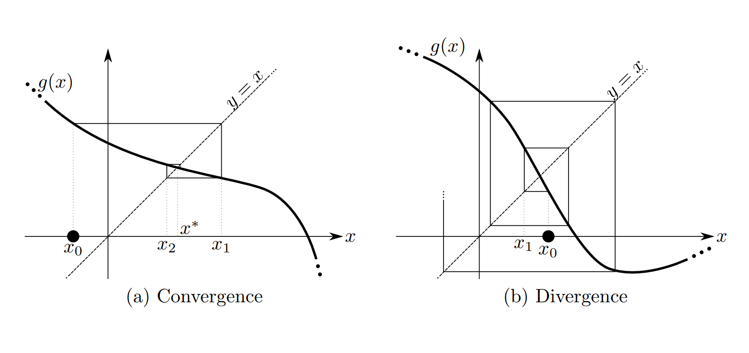
解法:
迭代法:令 xk+1=f(xk),直到 ∣xk−xk+1∣<ε (前提条件:f 满足 Lipschitz 条件)
由于迭代法往往是按照平方收敛的,所以其收敛速度往往更快。
3. 牛顿法
解方程 f(x)=0
可以使用牛顿法:
xk+1=xk−f′(xk)f(xk)
要求: f 在 xk 附近是可微的,且 f′(x∗)=0
4. Secant 法
解方程 f(x)=0
可以使用 Secant 法:
xk+1=xk−f(xk)−f(xk−1)f(xk)(xk−xk−1)