线性算法

以下假定所有讨论的矩阵都是方阵，且 $A\vec{x}=\vec{b}$ 一定可解。

1. Permutation

记 $\sigma : \{1,\cdots,m \}\to \{1,\cdots,m\}$

取矩阵 $P_\sigma$，对矩阵进行 Permutation 只需要 $P_\sigma A$ 即可

2. Row Scaling

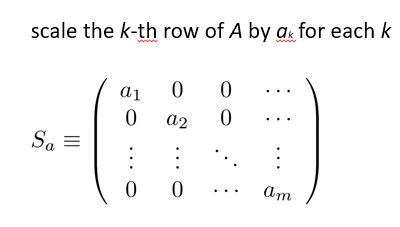
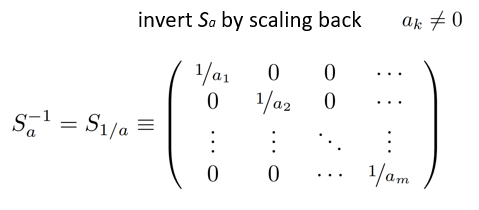故 Row Scaling 过程即为 $S_aA$

3. Elimination

令 $\vec{e_k}^T$ 的第 $k$ 位为 1，其他位均为 0，则取出 $A$ 的第 i 行并且移到第 j 行，可以表示为 $\vec{e_j}\vec{e_i}^TA$

4. LU 分解

对矩阵 $A$ 进行 LU 分解，$A=LU$，其中 $L$ 为下三角矩阵，$U$ 为上三角矩阵。

这样，就可以将 $Ax=b$ 转化为 $Ly=b,Ux=y$ 的问题。