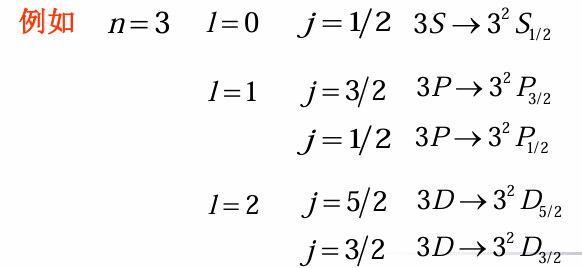1. 平均值与算符
1.1 粒子的位置 r
据波函数的定义,
⟨r⟩=∫−∞+∞ψ∗(r,t)rψ(r,t)dτ=⟨ψ∣r∣ψ⟩=⟨ψ∣r^∣ψ⟩
⟨ψ∣r^∣ψ⟩ 这种记号为狄拉克算符
位置的标准差为位置的不确定度 Δx
Δx=⟨x2⟩−⟨x⟩2
1.2 动量 p
⟨p⟩=⟨φ∣p∣φ⟩=⟨ψ∣p^∣ψ⟩
其中 p^=−iℏ∇,为动量算符
1.3 矢量算符
位置算符:x^ψ(x)=xψ(x)
动量算符:p^ψ=−iℏ∇ψ
动能算符:K^=2mp^2
势能算符:V^ψ(x)=V(x)ψ(x)
角动量算符:L^=r^×p^
此时可以将哈密顿算符记为 H^=2mp^2+V(r)
任意力学量 A 的期望(平均)值 ⟨A⟩=⟨ψ∣A^∣ψ⟩
其中 ψ 为表象,A^ 为表象下的算符形式
1.3.1 本征函数
若算符 A^ 作用在波函数 ψ 上得到的结果是一个常数乘以 ψ,即
A^ψ=aψ
则 ψ 是算符 A^ 的本征函数,a 是算符 A^ 的本征值。该方程称为算符 A^ 的本征方程。
1.3.2 对易式
两个算符 A^ 和 B^ 的对易式为
[A^,B^]=A^B^−B^A^
显然,
[x^,px^]=iℏ
若算符 A^ 和 B^ 对易,则 [A^,B^]=0,它们有共同的本征函数。
运算规律:
- [A^,B^C^]=[A^,B^]C^+B^[A^,C^]
- [A^+B^,C^]=[A^,C^]+[B^,C^]
[!NOTE]
对于任意函数 F(r),有 [p^,F]=p^F(r)
1.3.3 算符的逆
若算符 A^ 有逆算符 A^−1,则有
A^A^−1=A^−1A^=I^
1.3.4 算符的复共轭
算符 A^ 的复共轭 A^∗ 定义为
⟨ψ∣A^∣φ⟩=⟨φ∣A^∗∣ψ⟩
即将 A^ 中的所有复量换成共轭复量。
1.3.5 算符的转置
算符 A^ 的转置 A^ 定义为
⟨ψ∣A^∣φ⟩=⟨φ∣A^∣ψ⟩
1.3.6 算符的厄米共轭
算符 A^ 的厄米共轭 A^+ 定义为
⟨ψ∣A^∣φ⟩=⟨φ∣A^+∣ψ⟩
前后相逆,厄米居中。
即 A^+=A^∗
若 A^=A^+,则称 A^ 为厄米算符。内积形式 :(u,A^v)=(A^+u,v)
厄米算符可观测。
结论:
- 位置算符是厄米算符
- 动量算符是厄米算符
- 动能算符是厄米算符
1.3.7 力学量能互相确定的条件
若两个力学量算符 A^ 和 B^ 能互相确定的充要条件是它们对易,即 [A^,B^]=0。
1.4 时间演化算符
设 U^(t,t0) 是时间演化算符,满足
U^(t,t0)ψ(t0)=ψ(t)
则有
ψ(t)U^(t,t0)=U^(t,t0)ψ(t0)=e−ℏiE(t−t0)
其中 H^ 为哈密顿算符
2. 角动量算符
2.1 轨道角动量算符
设 L^=r^×p^,有
L^xL^yL^z=y^p^z−z^p^y=z^p^x−x^p^z=x^p^y−y^p^x
或者写成 L^j=εjklx^kp^l,其中 εjkl 是 Levi-Civita 符号。(重复指标求和)
εxyzεxzyεxxy=1=−1=0
定义角动量平方算符 L^2=L^x2+L^y2+L^z2
其对易关系:
- [Lx^,Ly^]=iℏLz^,进一步地使用形式的行列式可得 L^×L^=iℏL^
- [L^2,L^j]=0,即 L^2 和 L^j 互相确定
- [L^x,x^]=−iℏy^,[L^y,x^]=iℏz^,[L^z,x^]=0
- [L^x,p^x]=0,[L^y,p^x]=−iℏp^z,[L^z,p^x]=iℏp^y
2.2 角动量的本征方程
在球坐标系中,变量为 r^,θ^,ϕ^,可得球坐标中角动量的分量形式。
-
考虑本征方程 L^zψ=λψ,求得 ψ=Ceℏiλφ,由于周期性,ψ(0)=ψ(2kπ),得本征值 λm=mℏ,这就得到了角动量量子化的结论。
-
考虑本征方程 L^2ψ=λψ,可得本征值 λ=l(l+1)ℏ2,其中 l=0,1,2,⋯,m=−l,−l+1,⋯,l−1,l.
球谐函数
Ylm(θ,φ)=2π1NlmPlm(cosθ)eimφ
结论:
- 球谐函数系 Ylm(θ,φ) 是 L^2 和 L^z 的共同本征函数系 L^2YlmL^zYlm=l(l+1)ℏ2Ylm=mℏYlm
- 简并度为 2l+1,即 m=−l,−l+1,⋯,l−1,l.'
- 在球谐函数系下,⟨L^x⟩=⟨L^y⟩=0,⟨L^x2⟩=⟨L^y2⟩=2l(l+1)−mℏ2
3. 态叠加原理
具有确定动量粒子的波函数为平面波:
ψ(x)=2πℏ1eℏipx
如果动量不确定,则为平面波的叠加 – 傅里叶变换:
ψ(x)=2πℏ1∫−∞∞C(p)eℏipxdp
其中,
C(p)=2πℏ1∫−∞∞ψ(x,t)e−ℏipxdx
本征态 u 下测量 A,测量结果为确定的唯一的值 λ,理解方法:
- ∣Ci∣=1,其它地方 Cj=0,因此唯一确定;
- ΔA=⟨A2⟩−⟨A⟩2=0.
4. 氢原子
对于氢原子薛定谔方程 H^ψ=Eψ,化为球坐标系可得
ψ(r,θ,φ)=Rnl(r)Ylm(θ,φ)
且 H^,L^2,Lz^ 是彼此对易的,构成力学量完全集。
记 ψnlm 为氢原子波函数,n 为主量子数,l 为角量子数,m 为磁量子数。此时能级的简并度 g=n2
笔记:态与算符的矩阵表示
From Ch3 - 量子力学深入
[!Note]
狄拉克符号
波函数在不同表象中的表示
- ψ(x) 是波函数在 位置 表象中的表示;
- C(p) 是波函数在 动量 表象中的表示;
- Ψ=∑ncnψn,其中 ψn 是属于 能量 En 的定态波函数,则 c1⋯cn⋯ 称为波函数在 能量 表象中的表示。
- 对于厄密算符 F^ 来说,设 un 是属于厄密算符 F^ 的本征值 λn 的本征波函数,则称 c1,⋯,cn⋯ 称为波函数在 F 表象中的表示。
狄拉克符号表示态矢
根据态叠加原理,由于波函数的叠加性,称波函数为态矢,用狄拉克符号表示态矢,独立于表象
- ψ→∣ψ⟩ 称为右矢;波函数 → 态矢。
- ψ∗→⟨ψ∣ 称为左矢;波函数的复数共轭 → 态矢。
- 常用量子数表示态矢。
态矢的运算也符合 交换律、结合律、分配律。
内积 表示为:
⟨ψ1∣ψ2⟩=∫ψ1∗ψ2dx
因此:
-
态矢归一化可以表示为 ⟨ψ∣ψ⟩=1;
-
两个态矢相互正交可以表示为 ⟨ψ∣ϕ⟩=0.
-
基矢 {∣ψn⟩,n=1,2,⋯} 的正交归一完备性可以表示为:
⟨ψm∣ψn⟩=δmnn∑∣ψn⟩⟨ψn∣=I
-
若 ∣Ψ⟩=∑ncn∣ψn⟩,则:
⟨ψi∣Ψ⟩=n∑cn⟨ψi∣ψn⟩=ci⇒cn=⟨ψn∣Ψ⟩
-
∣Ψ⟩ 态下测量 A 的期待值(算符 A 的期待值)
⟨A⟩=⟨Ψ∣A^∣Ψ⟩
算符的定义与薛定谔方程
A^∣u⟩=∣v⟩A^∣u⟩=λ∣u⟩H^∣n⟩H^∣ψ(t)⟩=En∣n⟩=iℏ∂t∂∣ψ(t)⟩(定态)(含时)
狄拉克符号表示态矢的外积
(∣u⟩⟨v∣)∣ψ⟩=∣u⟩⟨v∣ψ⟩=(⟨v∣ψ⟩)∣u⟩
作用在任意右矢 ∣ψ⟩ 的结果是右矢,所以 ∣u⟩⟨v∣ 是算符。总结:
- ⟨u∣v⟩ 是常数;
- ⟨u∣A^∣v⟩ 是常数;
- ∣u⟩⟨v∣ 是算符。
例题 若 {∣ψn⟩,n=1,2,⋯} 是正交归一完备的基矢。求证 ∑n∣ψn⟩⟨ψn∣=I.
n∑∣ψn⟩⟨ψn∣ψ⟩=n∑⟨ψn∣ψ⟩∣ψn⟩=ψ
例题 对于任何两个代表不同状态的态矢量 ∣ψ⟩ 及 ∣φ⟩(未归一化),试证明下列 Schwarz 不等式:
∣⟨ψ∣φ⟩∣2<⟨ψ∣ψ⟩⟨φ∣φ⟩
等于证明:
⟨φ∣ψ⟩⟨ψ∣φ⟩<⟨ψ∣ψ⟩⟨φ∣φ⟩
证明:令⟨ψ∣ψ⟩=a(>0),⟨φ∣φ⟩=b(>0),⟨ψ∣φ⟩=c,并令
∣χ⟩=∣φ⟩−ac∣ψ⟩
由于 ψ,φ 代表不同状态,所以 ∣χ⟩=0,⟨χ∣χ⟩>0,即
⟨χ∣χ⟩=(⟨φ∣−ac∗⟨ψ∣)(∣φ⟩−ac∣ψ⟩)=b−ac∗c>0
所以 c∗c,亦即 ⟨ψ∣φ⟩∣2<⟨ψ∣ψ⟩⟨φ∣φ⟩.
例题 假如 ∣α⟩ 是一个归一化的态矢,算符 P^
P^≐∣α⟩⟨α∣
称为投影算符。证明
-
投影算符是等幂的:P^2=P^.
使用右矢 ∣ψ⟩ 作用,可得
P^2ψ=∣α⟩⟨α∣α⟩⟨α∣ψ⟩=∣α⟩⟨α∣ψ⟩=P^ψ
-
P^ 是厄密算符吗?
P^†=(∣α⟩⟨α∣)†=(⟨α∣†∣α⟩†)=∣α⟩⟨α∣
-
求出 P^ 的本征值,描述它的本征矢量。
假设 P^ψ=λψ,则 P^2ψ=λ2ψ=P^ψ=λψ,因此 λ=1 或 λ=0.
- λ=1:∣α⟩⟨α∣ψ⟩=∣ψ⟩=⟨α∣ψ⟩∣α⟩.
- λ=0:⟨α∣ψ⟩=0.
波函数的矩阵表示
右矢的矩阵表示
力学量完全集 F 所有共同本征函数 ∣un⟩ 构成一个完备正交的基矢,这样任何一个态矢 ∣ψ⟩ 都可以展开为:
∣ψ⟩=n∑cn∣un⟩
用 cn=⟨un∣ψ⟩ 描述体系状态。
∣ψ⟩=c1c2⋮
⟨ψ1∣ψ2⟩=m∑cm∗dm
各基矢 ∣un⟩ 在自身表象中的矩阵形式为:
∣u1⟩=10⋮,∣u2⟩=010⋮,⋯,∣un⟩=0⋮10⋮
cn 是态矢量 ∣ψ⟩ 在各基矢方向的分量,如同坐标分量。
∣ψ⟩=c1c2⋮=c1∣u1⟩+⋯+cn∣un⟩+⋯cn=⟨un∣ψ⟩
左矢和内积的矩阵表示
左矢的矩阵表示:cn∗ 排成一个行向量来表示
Ψ∗(x)=n∑cn∗un∗(x)⇒⟨ψ∣=(c1∗,c2∗,⋯)
矩阵的运算规则满足波函数的叠加性。
内积的矩阵表示:相当于做矩阵乘法。
可以证明
⟨ψ∣φ⟩=⟨φ∣ψ⟩∗

∣ψ1⟩=10⋮,∣ψ2⟩=010⋮,∣Ψ(x,t)⟩=e−iE2/h/2e−iE1/h/20⋮,∣Ψ∗(x,t)⟩=(eiE2/h/2eiE1/h/20⋯)
光子偏振态矢
算符的矩阵表示
对于一个算符 A^ 来说, 其可以用矩阵描述,其矩阵元素为:
Amn=∫um∗A^unda=⟨um∣A^∣un⟩
A^→A11⋮A12A22⋯⋱
共轭算符及其矩阵表示
定义算符 A^ 的共轭算符 A^†,A^ 与 A^† 互为共轭。
∫u∗A^vdx=∫(A^†u)∗vdx∫u∗A^†vdx=∫(A^u)∗vdx
共轭算符 A^† 矩阵是 A^ 矩阵的 转置+复数共轭,矩阵元 Amn†(第 m 行,第 n 列)
Amn†=⟨um∣A^†∣un⟩=∫um∗A^†undx=(∫(A^†un)∗umdx)∗=(∫un∗A^umdx)∗=⟨un∣A^∣um⟩∗=Anm∗
共轭算符的运算法则
(A^†)†=A^(A^∣u⟩)†=⟨u∣A^†(λA^)†=λ∗A^†(A^+B^)†=A^†+B†(A^B^)†=B†A^†
厄密算符的矩阵表示
A是厄密矩阵⇔A†=A⇔Amn=Anm∗
例题 证明假如相应于可观测量 A 的算符 A^ 是厄密算符,则 ⟨A2⟩≥0.
⟨A2⟩=⟨ψ∣A2∣ψ⟩=A∣ψ⟩:=u⟨ψ∣A∣u⟩=⟨ψ∣A†∣u⟩=(A∣ψ⟩)∗∣u⟩=⟨u∣u⟩≥0
算符期待值的矩阵表示
左矢是右矢的转置+共轭
∣Ψ⟩=c1c2⋮,⟨Ψ∣=(c1∗c2∗⋯)⟨A⟩=(c1∗c2∗⋯)A11⋮A12A22⋯⋱c1c2⋮
本征方程的矩阵表示
A11A12A22⋯...c1c2⋮⋮=λc1c2⋮⋮
求解 λ:
A11−λA12A22−λ......=0
定态薛定谔方程的矩阵表示
H11H12H22...⋯c1c2⋮⋮=Ec1c2⋮⋮
E 为 H 矩阵的特征值。
含时薛定谔方程的矩阵表示
H11H12H22......c1(t)c2(t)⋮⋮=iℏ∂t∂c1(t)c2(t)⋮⋮
初始条件:已知 Ψ(0)=c1(0)c2(0)⋮⋮.
例题 设 ∣u⟩,∣v⟩ 为态矢,⟨u∣u⟩ 即 ⟨v∣v⟩ 有限,证明:
Tr∣u⟩⟨v∣=⟨v∣u⟩
Tr∣u⟩⟨v∣=n∑⟨un∣u⟩⟨v∣un⟩=n∑⟨v∣un⟩⟨un∣∑=Iu⟩=⟨v∣u⟩


例题 设相应于一个例子的物理量的算符 A^ 只有两个本征函数 ϕ1(x) 和 ϕ2(x),他们的本征值分别为 a1 和 a2,两者不等,粒子的任一一个态都可以表示为:
ψ=c1ϕ1(x)+c2ϕ2(x)
算符 B^ 定义为:
B^ψ=c2ϕ1(x)+c1ϕ2(x)
-
证明算符 B^ 是厄密算符。
(B11B21B12B22)(c1c2)=(c2c1)
B=(0110)
-
求算符 B^ 的本征值以及相应的归一本征函数。
λ2−1=0⇒λ=±1
归一本征函数:
u1=21(11)u−1=21(1−1)
-
若粒子处于态 ψ=31ϕ1(x)+31−iϕ2(x),求在该态下测量 B 的期待值。
⟨B⟩=(3131+i)(0110)(3131−i)=32
5. 自旋
5.1 SG 实验
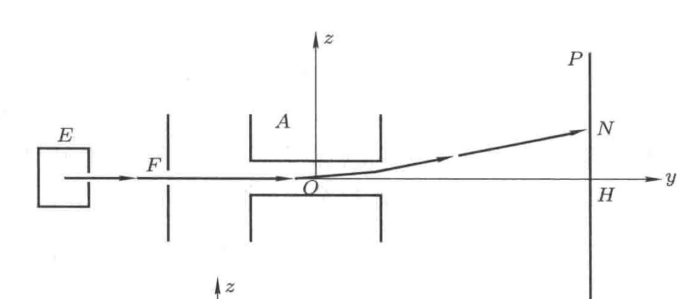 s 态(l=0)的银原子束流,经非均匀磁场发生偏转,在感光板上呈现两条分立线。
s 态(l=0)的银原子束流,经非均匀磁场发生偏转,在感光板上呈现两条分立线。
结论:
银原子有磁矩,且只有两种取向
5.2 电子自旋假设
- 自旋是微观效应的固有属性,不能用宏观的自旋对应。否则电子自转的速度将大于光速。
- 自旋角动量,用 S 表示,Si(i=x,y,z) 分别代表它的是三个分量。自旋角动量算符的分量和轨道角动量有相同的对易关系。
- Sz=±2ℏ,电子的自旋磁矩与自旋角动量的关系为:
Ms=−μeS
其中 μ 为电子的磁矩,e 为电子的电荷量。
回转磁比率
- 电子回转磁比率 SzMSz=−μe
- 轨道回转磁比率 −2μe
5.3 自旋算符和自旋波函数
5.3.1 自旋算符
使用算符 S^ 描述自旋角动量。
[S^i,S^j][S^x,S^y][S^y,S^z][S^z,S^x][S^2,S^i]=iℏεijkS^k=iℏS^z=iℏS^x=iℏS^y=0
自旋角动量 S^x S^y S^z 的本征值都是 ±2ℏ
5.3.1 含自旋的波函数
5.4 泡利矩阵
记升状态为 χ+,降状态为 χ−
χ+=(10), χ−=(01)
泡利矩阵是描述自旋的算符,定义为
σ^x=(0110), σ^y=(0i−i0), σ^z=(100−1)
其中 σ^x,σ^y,σ^z 分别对应自旋角动量算符 S^x,S^y,S^z。
定义 S±=Sx±iSy,则有 S±=21(σx±iσy).(并非厄米算符)
6. 原子光谱的精细结构
6.1 电子的角动量
J=L+S
其中 J 为总角动量,L 为轨道角动量,S 为自旋角动量。
其中 j=l±21,其中 j 为总角量子数,l 为轨道角量子数。j 满足 ∣l−s∣≤j≤l+s
磁量子数 mj 的取值范围为 −j,−j+1,⋯,j−1,j,简并度为 2j+1.
6.2 磁矩
描述原子电子态
使用符号 nSj, 其中 n 表示主量子数;S 表示自旋状态,s 对应 l=0,p 对应 l=1 ; j 表示总角动量量子数。
认为原子的总磁矩为 μB=μl+μs,其中 μl 为轨道磁矩,μs 为自旋磁矩。
磁矩的计算公式:μ=−mgμB,其中 g 因子对于自旋为 gs=2,对于轨道为 gl=1. 对于 gj 要独立计算。
有效磁矩指的是原子在外磁场中产生的磁矩,定义为
μj=−gJℏμBJ=−mjgjμB
其中 gJ 为朗德因子,gJ=1+2j(j+1)j(j+1)−l(l+1)+s(s+1),j=l+s。
6.3 弱磁场下原子能级的分裂
在外磁场 B 下,原子能级会发生分裂。分裂的能级数目为 2j+1,能量变化为
ΔE=−μj⋅B=gJμBmjB
其中 mj 为磁量子数,B 为外磁场的强度。
跃迁选择定则:在磁场中,原子跃迁的选择定则为 Δmj=0,±1
7. 碱金属双线
- 能级由 n,j,l 三个量子数决定。当 l=0 时,j=s,能级不分裂;当 l=0 时,j=l±21,能级分裂为双层。
ΔEl,s=2n3(2l+1)Rchα2Z∗4{l+11>0,−l1<0,j=l+21j=l−21
- 能级分裂的间隔由 n,l 决定,δEn,l=2n3l(l+1)Rhcα2Z∗4
- 双层能级中,j 越大的能级越高
- 单电子辐射跃迁的选择定则:Δl=±1,Δj=0,±1
- 碱金属原子态符号 nL→n2s+1Lj
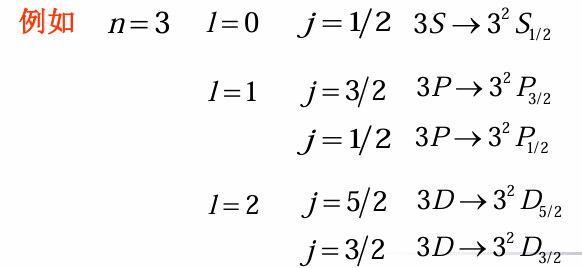
 态()的银原子束流,经非均匀磁场发生偏转,在感光板上呈现两条分立线。
态()的银原子束流,经非均匀磁场发生偏转,在感光板上呈现两条分立线。