跳到主要内容

Pauli 不相容原理

1. 能级缺失​

1.1 电子组态​

处于一定状态的若干个（价）电子的组合。

电子组态的表示：

  • 单个电子: nlnl
  • 两个电子: n1l1n2l2n_1l_1n_2l_2

1.2 双电子耦合​

400

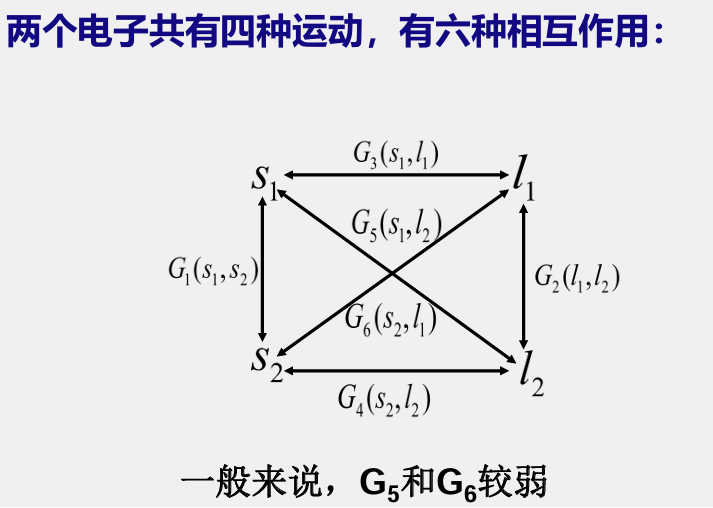
1.3 两电子的原子态​

以下主要说明 LS 耦合

450

[!NOTE] 此处的总量子数取值从 L−SL-S 到 L+SL+S

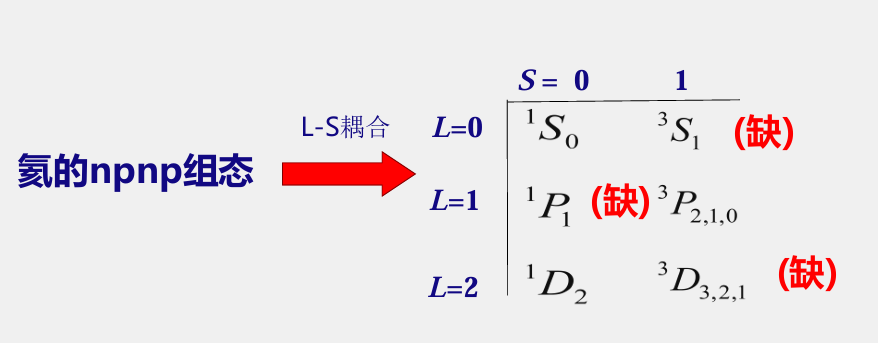
1.4 能级缺失​

耦合后的态并非 L×SL\times S 种，而是会缺失一部分。

例如，氦的 npnp 组态： 400

2. 泡利不相容原理​

[!Note] 同科电子的偶数定则：L+SL+S 必为偶数

2.1 洪特定则​

  1. SS 越大，能级越低
  2. SS 相同，LL 值越大，能级越低
  3. 同科电子，LL 相同，
    • 同科电子数 ⩽\leqslant 闭壳层占有数的一半，JJ 越小，能级越低
    • 同科电子数 >> 闭壳层占有数的一半，JJ 越大，能级越低

3. 全同粒子​

3.1 全同粒子​

质量、电荷、自旋等固有性质完全相同的微观粒子。

在波函数重叠区，粒子不可区分。

3.2 全同性原理​

单粒子波函数用 ψ(x)\psi(x) 描述，而多粒子体系波函数用 ψ(x1,x2,⋯ ,xn)\psi(x_1,x_2,\cdots,x_n) 描述。

定义交换算符，就是把粒子 1 的所有坐标（标识）与粒子 2 交换。

全同性原理要求交换算符作用后描述同一状态，即相差一常数。

P12Ψ(1,2)=Ψ(2,1)=λΨ(1,2)P_{12}\Psi(1,2)=\Psi(2,1)=\lambda \Psi(1,2)

因为 P122Ψ(1,2)=Ψ(1,2)=λ2Ψ(1,2)P_{12}^2\Psi(1,2)=\Psi(1,2)=\lambda^2\Psi(1,2)，所以 λ=±1\lambda=\pm 1.

  • λ=1\lambda=1，交换对称，用 ΨS(1,2)\Psi_{S}(1,2) 表示；
  • λ=−1\lambda=-1，交换反对称，用 ΨA(1,2)\Psi_{A}(1,2) 表示。

例如，对于波函数 ψ(x1,x2)=ϕ1(x1)ϕ2(x2)+ϕ1(x2)ϕ2(x1)\psi(x_1,x_2)=\phi_1(x_1)\phi_2(x_2)+\phi_1(x_2)\phi_2(x_1)，是交换对称的，ψ(x1,x2)=ϕ1(x1)ϕ2(x2)−ϕ1(x2)ϕ2(x1)\psi(x_1,x_2)=\phi_1(x_1)\phi_2(x_2)-\phi_1(x_2)\phi_2(x_1)，是交换反对称的。

根据自旋量子数，微观粒子分为费米子和玻色子。

  • 费米子，自旋为半整数，s=12,32,⋯s=\displaystyle \frac{1}{2},\frac{3}{2},\cdots。
    • 如电子，质子，中子；
    • 满足泡利不相容原理。
  • 玻色子，自旋为整数，s=0,1,⋯s=0,1,\cdots.
    • 如光子，胶子，α\alpha 粒子（氦核）
    • 不满足泡利不相容原理。

组成物质的基本粒子是费米子，传递相互作用的媒介子是玻色子。