1. 光的波粒二象性
- 光的波动性:光在光源和探测器之间以概率波的形式传播,概率波具有叠加性,p∝∣E∣2.
- 光的粒子性:光以光子的形式产生,光是由光子组成的能量流,光作为光子在探测器中被吸收。可以测量光子的能量,动量,角动量。
2. 物质波
2.1 德布罗意关系
Ep=hν=λh
2.2 物质波的实验验证
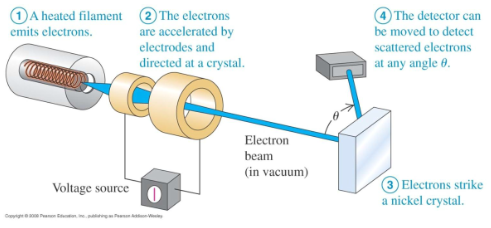
经过电压 U,考虑相对论效应,得
λ=2meU+c2e2U2h
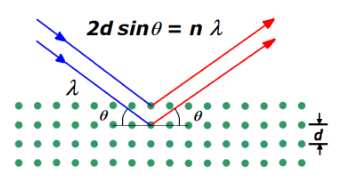
nλ=2dsinθ
3. 波函数
3.1 波函数的统计意义
类比具有确定频率的光子, 具有确定动量与能量的自由粒子的波函数为平面波 ψ(r,t)
则波函数表示为
Ψ(x,t)=ψ0⋅ei(px−Et)
粒子的状态由 ψ(x) 描述。粒子出现在位置 𝑥 处的位置 概率振幅 就是波函数 ψ(x)。
-
测量到粒子出现在 [x,x+dx] 区间的概率
dP=∣ψ(x)∣2dx
-
位置概率密度:
ρ(x)=∣ψ(x)∣2=ψ∗(x)ψ(x)
-
粒子出现在有限间隔 [a,b] 的概率:
Pab=∫abρ(x)dx
3.2 波函数的乘积与叠加
波函数的乘积: 如果一个事件的发生过程可以看成是 分几步发生, 比如光的不相符实验中光子先从光源到达分光器, 再从分光器到达光电倍增管, 则波函数应该是每一步对应的波函数的乘积.
波函数的叠加性: 如果一个事件的发生是可以 通过多种途径发生, 比如双缝实验中测量光子出现在某个位置, 则波函数应该是所有可能途径的波函数的叠加。
3.3 波函数的条件
- 连续性:波函数及其导数在空间中是连续的。
- 有限性:波函数在任意区间 [a,b] 内平方可积。
∫ba∣ψ(x)∣2dx<∞
3.4 不确定性关系
- 位置不确定性:ΔxΔp≥2ℏ。
- 能量不确定性:ΔEΔt≥2ℏ。
4. 薛定谔方程
含时薛定谔方程:
iℏ∂t∂Ψ(r,t)=(−2mℏ2∇2+V(r,t))Ψ(r,t)
其中 ∇2 是拉普拉斯算子:
∇2=∂x2∂2+∂y2∂2+∂z2∂2
4.1 定态薛定谔方程
设 Ψ=ψe−ℏiEt
则有
Eψ=(−2mℏ2∇2+V)ψ
含时薛定谔方程的一般解为:
Ψ(r,t)=n∑cnψne−ℏiEnt
其中 cn 为待定系数,为常复数
5. 一维定态问题
5.1 无限深势阱
无限深势阱的势能 V(x) 满足
V(x)={0,∞,0<x<aotherwise
解薛定谔方程,得
ψ(x)=a2sin(anπx)
能级 En 表达式为:
En=2ma2n2π2ℏ2
5.2 有限深势阱
有限深势阱的势能 V(x) 满足
V(x)={−V0,0,0<x<aotherwise
解薛定谔方程,得
ψ(x)k=Aeikx+Be−ikx=ℏ22mE
对于有限深势阱,必然存在束缚态
5.3 一维方势垒
设势能 V(x) 满足
V(x)={V0,0,0<x<aotherwise
5.4 一维谐振子
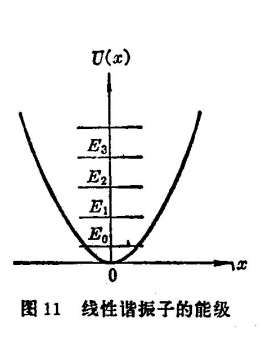
一维谐振子的势能 V(x) 满足
V(x)=21mω2x2
故定态薛定谔方程为
Eψ(x)=(−2mℏ2dx2d2+21mω2x2)ψ(x)
记 α=ℏmω , ξ=αx,λ=ℏω2E,则有
dξ2d2ψ=(ξ2−λ)ψ
得到能量本征函数 ψn(x)=Nne−21ξ2Hn(ξ)
其中 Hn(ξ) 是 Hermite 多项式,Nn 是归一化常数。
解法:(升降算符)
记算符 a−^=21(x^+ip^),a+^=21(x^−ip^),则有
a−^ψna+^ψn=nψn−1=n+1ψn+1
且 H^=ℏω(a−^a+^−21),[a−^,a+^]=1
而 H^a^+ψ=(E+ℏω)a^+ψ,H^a^−ψ=(E−ℏω)a^−ψ
由 a^−ψ0=0,可得 ψ0=π411e−21ξ2


