1. 黑体辐射
1.1 测量黑体辐射的物理量
单色辐出度 M(λ,T) 是单位面积单位波长范围内的辐射功率,单位是 W⋅m−2⋅nm−1
定义为:
M(λ,T)=dλdE
吸收比 α(T) 是单位面积单位波长范围内的吸收功率与辐射功率之比:
α(T)=E入射E吸收
1.2 黑体辐射理论
1.2.1 斯特藩-玻尔兹曼定律
E0(T)=σT4
其中 σ=5.67×10−8W⋅m−2⋅K−4
1.2.2 维恩位移定律
λmT=b
其中 b=2.898×10−3m⋅K
1.3 普朗克能量子假设
1.3.1 普朗克能量量子假设
E=nhν
普朗克黑体辐射公式:
M(λ,T)=λ52πhc2eλkThc−11
(频率形式为)
M(ν,T)=c22πhν3ekThν−11
2 光电效应
2.1 爱因斯坦关系
E2=p2c2+m02c4
Ep=hν=λhc=λh
2.2 光电效应的实验规律
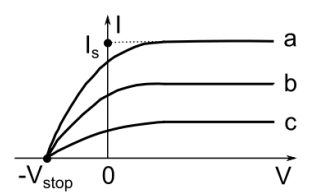
2.2.1 饱和电流
- 只有当光的频率超过某个阈值时,才有光电流。这个阈值称为红限(截止)频率,截止频率与金属板的材料有关.
- 当入射光的频率给定后,光电流正比于光强。在入射光强一定时光电流会随电压增大,最后达到一饱和值。饱和电流与入射光强成正比.
- 当电压为零时光电流并不为零,甚至反向电压不太大时仍有光电流存在。当反向电压大到一定数值 Ustop 时光电流完全变为零,称为遏止电压。遏止电压和入射光的频率存在线性关系。光电子的最大动能 Kmax=eUstop.
- 无论多弱的光强都没有观察到电子出射的延迟.
3. 康普顿散射
3.1 康普顿散射实验
1922-1923 年,美国物理学家康普顿将 X 射线射向实物物质,观察散射现象。

散射光中除了有原波长的 X 光外,还有波长更长的散射光,其波长的增量随散射角的增加而增加,且与物质材料无关。
3.2 康普顿散射公式
λ′−λ=mech(1−cosθ)
其中 λ 为入射光的波长,λ′ 为散射光的波长,θ 为散射角,me 为电子质量。
康普顿波长:λc=mech=2.43×10−12m
4. 波尔理论
4.1 20 世纪初的原子模型
- 1897 年,英国物理学家汤姆孙 (J.J. Thomson) 测量了阴极射线在电磁中的轨迹, 从而确定了电子的荷质比。
- 1910 年, 密立根完成油滴实验, 确定了电子的电荷量。
- 汤姆森的西瓜模型, 卢瑟福的核式模型。
- 卢瑟福散射实验:高速运动的 α 粒子垂直入射到金箔靶面上,发生散射。
- 原子核怎么保持稳定的讨论。
- 原子光谱(发射光谱、吸收光谱)
- 巴尔末公式 λ=Bn2−4n2
- 里德伯公式 v=R[(m+a)21−(n+b)21]
4.2 波尔原子模型
- 定态假设:电子只能够稳定地存在一系列状态中,这些状态称为定态 (stationary state);在定态下,电子不发射或吸收电磁辐射.
- 频率假设:电子在不同的允许轨道之间跃迁,导致原子释放出光谱线. 光谱线的频率 𝜈 由两个层级的能量差决定。
En−Em=hν
- 角动量量子化假设:电子在轨道上的角动量是量子化的,即
L=nℏ
4.3 波尔半径
rn=Zn2a0
其中 a0=mee2ℏ24πε0=0.529×10−10m 称为玻尔半径。
4.4 氢原子能级
En=−n2Z28πε0a0e2=−2mec2α2n2Z2=n2Z2E1
其中 α=1371,即为精细结构常数。
基态能量 E1=−13.6eV

