数论

1.1 基本算数

[!NOTE] 定理:任意三个一位数相加，和最多只有两位

• 加法计算的时间复杂度是 $O(n)$，其中 $n$ 为参与运算的数字位数

• 乘法计算的时间复杂度是 $O(n^2)$，其中 $n$ 为参与运算的数字位数 (第一章暂定)

• 带余除法计算的时间复杂度是 $O(n^2)$，其中 $n$ 为参与运算的数字位数

1.2 模运算

• 定义：$a \equiv b \mod m \iff m \mid (a-b)$

[!NOTE] 模运算支持除了除法以外的所有四则运算，这意味着：

• $(a+b) \mod m = ((a \mod m) + (b \mod m)) \mod m$
• $(a-b) \mod m = ((a \mod m) - (b \mod m)) \mod m$
• $(a \times b) \mod m = ((a \mod m) \times (b \mod m)) \mod m$
• $(a^b) \mod m = ((a \mod m)^b) \mod m$
• $(-a) \mod m = (m - (a \mod m)) \mod m$
• $(a/b) \mod m = ((a \mod m) \times (b^{-1} \mod m)) \mod m$，其中 $b^{-1}$ 为 $b$ 关于模 $m$ 的乘法逆元
• $a\equiv b \mod m \rightarrow \frac{a}{d} \equiv \frac{b}{d} \mod \frac{m}{d}$，其中 d 为 $a,b,m$ 的最大公约数

欧几里得最大公因数算法：

$$\gcd(a,b)=\gcd(b,a ~\text{mod}~b)$$

欧几里得算法的时间复杂度是 $O(n^3)$，其中 $n$ 为参与运算的数字位数

扩展欧几里得算法：

[!NOTE] 裴蜀定理 若 $d | a$ 且 $d|b$，且同时存在整数 $x,y$ 使得 $ax+by=d$，则 $d=\gcd(a,b)$

计算 $\gcd(x,y)$，可以采取以下步骤：

$$\begin{aligned} \underline {x} &= q\underline{y} + r \\ \underline y &= k\underline r + s \\ \underline r &= l\underline s + t \\ &\cdots \end{aligned}$$

乘法逆元

[!NOTE] 若 $ax\equiv 1\mod N$，则称 $x$ 为 $a$ 关于模 $N$ 的乘法逆元

若 $\gcd(a,N)=1$，则 $a$ 关于模 $N$ 的乘法逆元存在且唯一

1.3 素性测试

[!NOTE] 费马小定理 如果 $p$ 是素数，且 $a$ 是整数且不被 $p$ 整除，则有：

$$a^{p-1} \equiv 1 \mod p$$

引理：如果对于某些与 $N$ 互素的 $a$，有 $a^{N-1}/\!\!\!\!\!\!\equiv \mod N$，那么对于 $a<N$ 的至少一半的可能取值，$N$ 将无法通过费马测试

[!NOTE] Lagrange 素数定理 令 $\pi(x)$ 为不大于 $x$ 的素数个数，则当 $x \to \infty$ 时，有：

$$\pi(x) \sim \frac{x}{\ln x}$$

随机算法：

• 蒙特卡洛算法：运行很快，输出错误解的概率很低
• 拉斯维加斯算法：运行时间很快，输出正确解

1.4 密码学

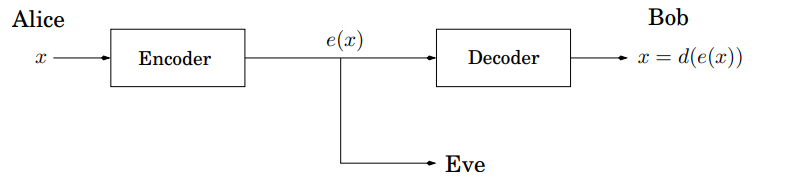
RSA 加密

随机选取两个不同的素数 $p$ 和 $q$，计算 $N=pq$ 和 $\phi(N)=(p-1)(q-1)$ 随机选取一个整数 $e$，使得 $1<e<\phi(N)$ 且 $\gcd(e,\phi(N))=1$，计算 $d$ 使得 $ed \equiv 1 \mod \phi(N)$ 令公钥为 $(e,N)$，私钥为 $(d,N)$