4.3 协方差及其相关系数

1. 协方差

1.1 定义

若期望 $E(X-E(X)(Y-E(Y)))$ 存在，则称之为 $X,Y$ 的==协方差==

记为

$$\begin{aligned} \operatorname{cov}(X, Y) &= E[(X-E(X))(Y-E(Y))] \end{aligned}$$

1.2 计算

2. 相关系数

2.1 定义

若 $D(X)>0, D(Y) > 0$，则称 $\rho_{XY}=\frac{\mathrm{cov}(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$ 为 $X,Y$ 的==相关系数==

相关系数描述了 $X,Y$ 之间==线性关系==的强弱。

2.2 性质

对于二维正态分布 $(X,Y)\sim N(\mu_1,\sigma_1;\mu_2,\sigma_2;\rho)$，$X$ 与 $Y$ 相互独立 $\iff$ $\rho=0$

3. 性质

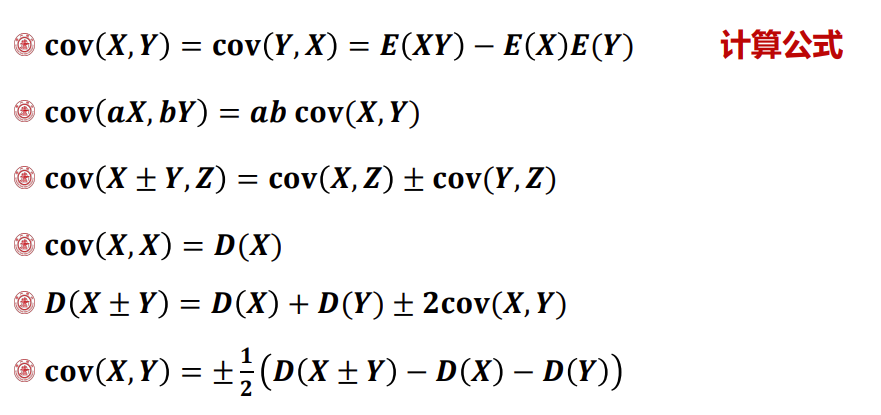
4. Cauchy-Schwarz不等式

$$\begin{aligned} \left|\operatorname{cov}(X,Y)\right| &\leq \sqrt{D(X)D(Y)} \end{aligned}$$

协方差理解为向量内积，方差理解为向量的 2-范数