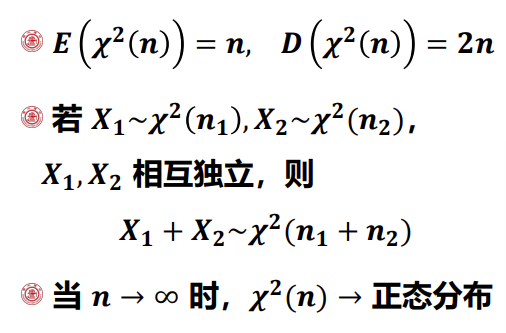6.2 抽样分布

1. 正态分布

2. $\chi^2$ 分布（卡方分布）

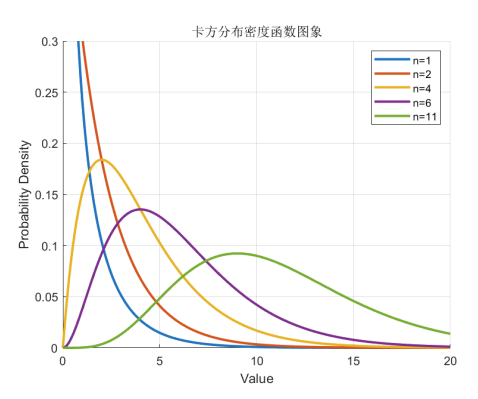
2.1 定义

设 $X_1,X_2,\cdots,X_n$ 独立同分布，且都服从标准正态分布 $N(0,1)$，则称随机变量

$$\begin{aligned} \chi^2 = X_1^2+X_2^2+\cdots+X_n^2 \end{aligned}$$

服从==自由度==为 $n$ 的 $\chi^2$ 分布，记为 $\chi^2\sim \chi^2(n)$。

其密度函数为

$$\begin{aligned} f(x)=\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}, x>0 \end{aligned}$$

其中 $\Gamma(x)$ 为 $\Gamma$ 函数。

注： $\chi^2(2)=E\left( \frac{1}{2} \right)$

设 $(X_1, X_2, \cdots, X_n)$ 是来自正态总体 $N(\mu,\sigma^2)$ 的样本，则

$$\begin{aligned} \frac{1}{\sigma^2} \sum_{i=1}^{n}(X_i-\mu)^2\sim \chi^2(n) \end{aligned}$$

假设其样本方差为 $s^2$，则

$$\begin{aligned} \frac{(n-1)s^2}{\sigma^2}\sim \chi^2(n-1) \end{aligned}$$

且 $\frac{(n-1)S^2}{\sigma^2}$ 与 $\overline{X}$ 相互独立。

2.2 性质

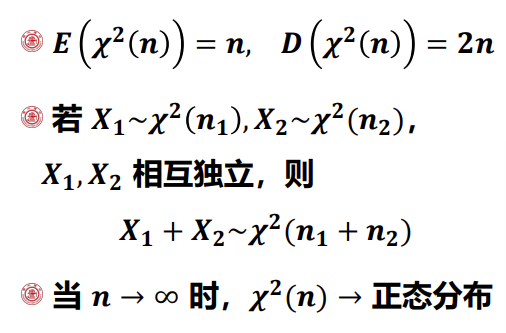
3. $t$ 分布（Student 分布）

3.1 定义

设 $X\sim N(0,1), Y\sim \chi^2(n)$，且 $X,Y$ 独立，则称随机变量

$$\begin{aligned} T=\frac{X}{\sqrt{Y/n}} \end{aligned}$$

服从自由度为 $n$ 的 $t$ 分布，记为 $T\sim t(n)$。

其密度函数为

$$\begin{aligned} f(t)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(1+\frac{t^2}{n})^{-\frac{n+1}{2}} \end{aligned}$$

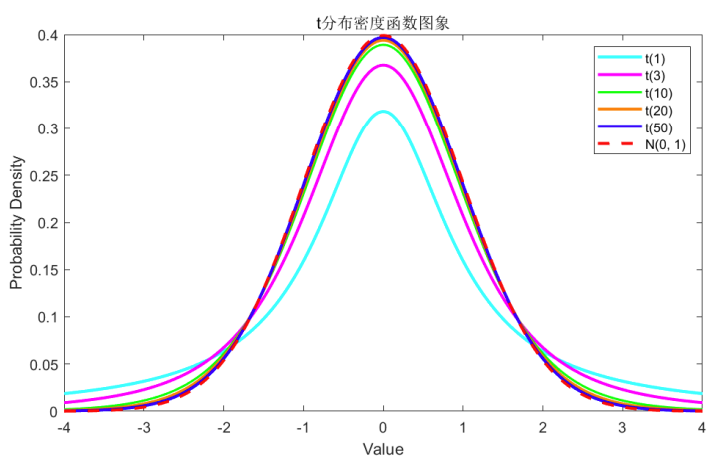
3.2 性质

• 当 $n=1$ 时，$t$ 分布即为柯西分布。其数学期望不存在。
• 当 $n>1$ 时，$t$ 分布的数学期望为 $0$，方差为 $\frac{n}{n-2}$。
• $t$ 分布的概率密度函数是偶函数，且当 $n\to\infty$ 时，$f(t)\to\varphi(t)=\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}$

4. $F$ 分布

4.1 定义

设 $X\sim \chi^2(m), Y\sim \chi^2(n)$，且 $X,Y$ 独立，则称随机变量

$$\begin{aligned} F=\frac{X/m}{Y/n} \end{aligned}$$

服从自由度为 $(m,n)$ 的 $F$ 分布，记为 $F\sim F(m,n)$。

其密度函数为

$$\begin{aligned} f(x)=\frac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{n}{2})}(\frac{m}{n})^{\frac{m}{2}}x^{\frac{m}{2}-1}(1+\frac{m}{n}x)^{-\frac{m+n}{2}} \end{aligned}$$

4.2 性质

• 若 $X\sim F(m,n)$，则 $\frac{1}{X}\sim F(n,m)$
• $F_{1-\alpha}(n,m)=\frac{1}{F_{\alpha}(m,n)}$
• 当 $n\to\infty$ 时，$F$ 分布趋近于正态分布