6.1 基本概念

1. 样本、总体和个体

2. 统计量

2.1 概念

2.2 常用统计量

设 $(X_1,X_2,\cdots,X_n)$ 是来自总体 $X$ 的容量为 $n$ 的样本，定义以下统计量

公式	名称
$\overline{X} = \frac{1}{n}\sum_{i=1}^{n}X_i$	样本均值
$S^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2$	样本方差
$S=\sqrt{\frac{1}{n-1}\sum^n_{i=1}(X_i-\overline{X})^2}$	样本标准差
$M_k = \frac{1}{n}\sum_{i=1}^n X_i^k$	样本的 $k$ 阶原点矩
$(CM)_k=\frac{1}{n}\sum^n_{i=1}(X_i-\overline{X})^k$	样本的 $k$ 阶中心矩

2.3 顺序统计量

2.4 中位数

2.5 注释与重要结论

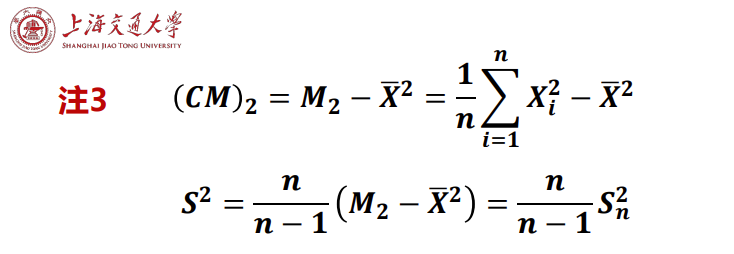
若总体 $X$ 的期望与方差存在，$E(X)=\mu,D(X)=\sigma^2$，则

$$\begin{aligned} E(\overline{X})&=\mu, \\ D(\overline{X})&=\frac{\sigma^2}{n} \\ E(S^2) &= \sigma^2 \\ D(S^2) &= \frac{2\sigma^4}{n-1} \end{aligned}$$

2.6 $\alpha$ 分位数

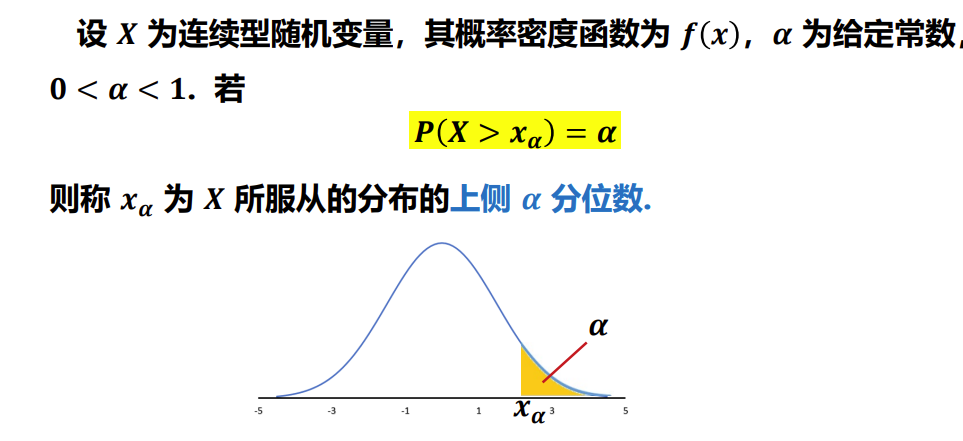
2.6.1 上侧 $\alpha$ 分位数

2.6.2 双侧 $\alpha$ 分位数

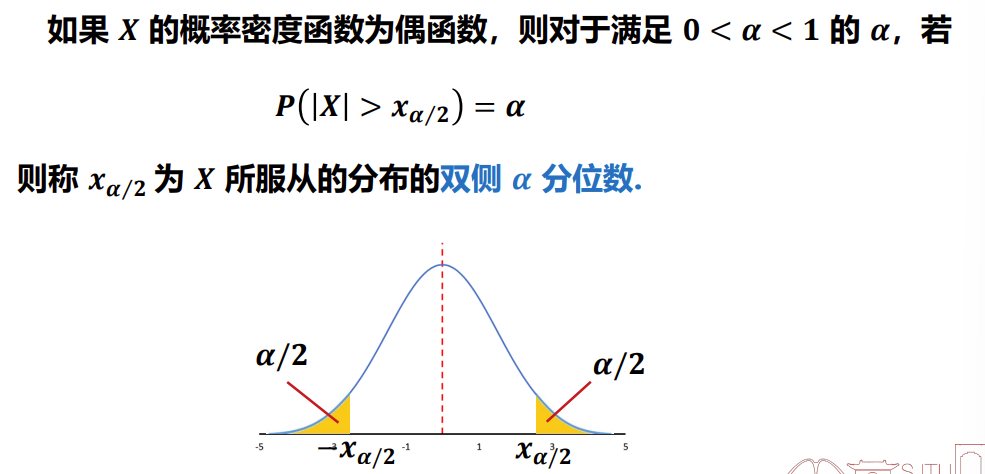
对于标准正态分布 $X\sim N(0,1)$，有

$$\begin{aligned} \Phi(-u_{\alpha})&=\alpha, \\ \Phi(u_{\alpha})&=1-\alpha,\\ \Phi(-u_{\alpha/2})&=\alpha/2, \\ \Phi(u_{\alpha/2})&=1-\alpha/2 \end{aligned}$$

常用值：$u_{0.05}=1.645, u_{0.01}=2.33, u_{0.025}=1.96, u_{0.005}=2.58$