跳到主要内容

3.1 二维随机变量及其分布

1. 二维随机变量​

1.1 定义​

设 Ω\Omega 是随机试验的样本空间，

∀ω∈Ω→按一定的对应法则→∃(X(ω),Y(ω))∈R2\forall \omega \in \Omega \to^{按一定的对应法则}\to \exists (X(\omega),Y(\omega)) \in \mathbb{R}^2

则称 (X,Y)(X,Y) 为二维随机变量（或二位随机向量）

2. 二维随机变量的联合分布函数​

2.1 定义​

设 (X,Y)(X,Y) 为二维随机变量，对于任意实数 (x,y)(x,y)，称定义在是平面上的二元函数

F(x,y)=P((X⩽x)∩(Y⩽y))=P(X⩽x,Y⩽y)F(x,y)=P((X\leqslant x)\cap(Y\leqslant y))=P(X\leqslant x, Y \leqslant y)

为二维随机变量 (X,Y)(X,Y) 的联合分布函数，也简称之为联合分布或分布函数

2.2 几何意义​

600

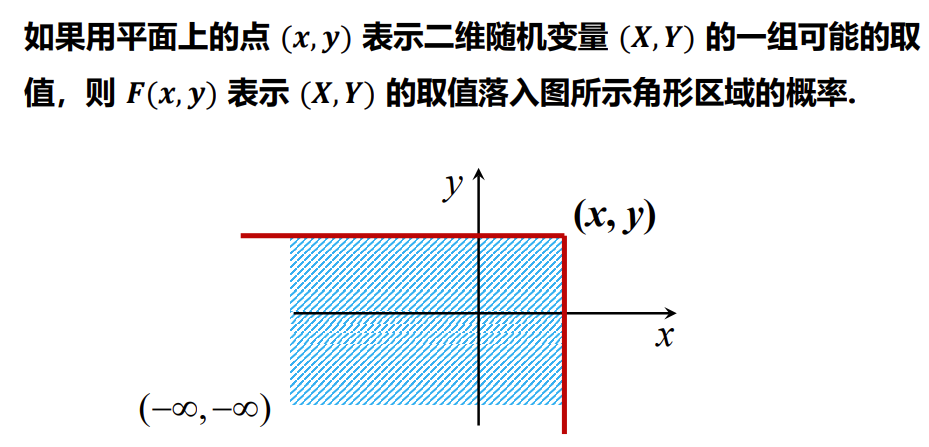
2.3 性质​

  • 0⩽F(x,y)⩽10\leqslant F(x,y) \leqslant 1
  • F(−∞,y)=0,F(x,−∞)=0,F(−∞,−∞)=0,F(+∞,+∞)=1F(-\infty, y)=0, F(x,-\infty)=0, F(-\infty,-\infty)=0, F(+\infty,+\infty)=1
  • F(x,y)F(x,y) 分别关于 xx 或 yy 单调不减
  • F(x,y)F(x,y) 分别关于 xx 或 yy 右连续
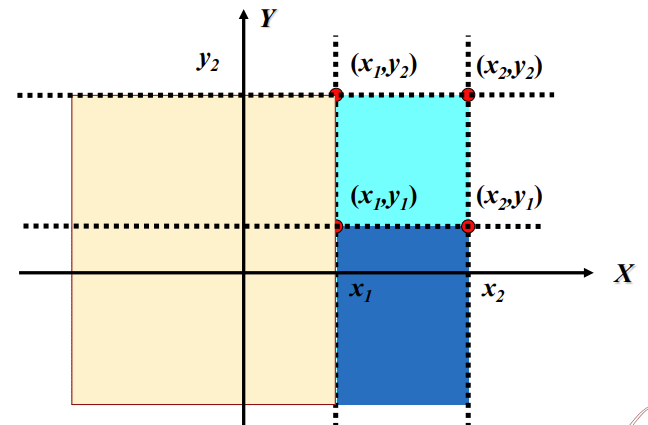
  • 对于 ∀x1<x2,y1<y2\forall x_1<x_2, y_1<y_2，有
F(x2,y2)−F(x2,y1)+F(x1,y1)−F(x1,y2)=P(x1⩽X⩽x2,y1⩽Y⩽y2)⩾0F(x_2,y_2)-F(x_2,y_1)+F(x_1,y_1)-F(x_1,y_2)=P(x_1\leqslant X\leqslant x_2, y_1\leqslant Y\leqslant y_2)\geqslant 0

撇减捺，恒非负

300

2.4 二维随机变量的边缘分布​

FX(x)=P(X⩽x)=F(x,+∞)F_X(x)=P(X\leqslant x)=F(x,+\infty) FY(y)=P(Y⩽y)=F(+∞,y)F_Y(y)=P(Y\leqslant y)=F(+\infty,y)

3. 二维离散型随机变量​

600

600 600

4. 二维连续型随机变量​

550

性质​

  1. 非负性：f(x,y)⩾0f(x,y)\geqslant 0
  2. 规范性：∫−∞+∞∫−∞+∞f(x,y)dxdy=1\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dx dy=1
  3. 设 (X,Y)(X,Y) 为二维连续型随机变量，则对平面上任意区域 DD，有
P((X,Y)∈D)=∬Df(x,y)dxdyP((X,Y)\in D)=\iint_D f(x,y)dx dy
  • Tips：面积为 0 的区域之概率为 0
  1. 在 (x,y)(x,y) 的连续点处有
f(x,y)=∂2F(x,y)∂x∂yf(x,y)=\frac{\partial^2 F(x,y)}{\partial x \partial y}

550

常见二维随机变量的分布​

1. 二维均匀分布​

550 550

2. 二维正态分布​

550

  • 正态分布的边缘分布仍然为正态分布。反之未必成立。